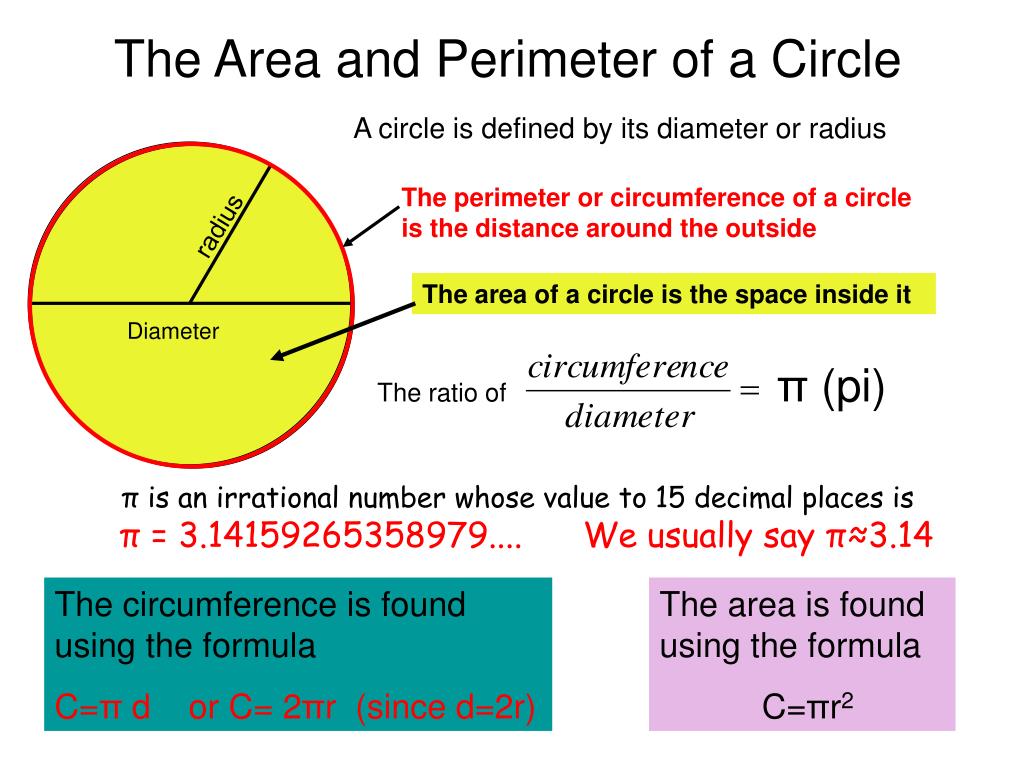
Diameter is the line that separates the circle into two equal parts and is also equal to twice the radius. A circle is a fundamental shape that is measured in terms of its radius. In geometry or mathematics, a circle can be defined as a special variety of ellipse in which the eccentricity is zero and the two foci are coincident. Circle is a particular shape and defined as the set of points in a plane placed at equal distance from a single point called the center of the circle. We use the circle formula to calculate the area, diameter, and circumference of a circle. Radius is half the length of a diameter of the circle.
Area of the circle describes the amount of space covered by the circle and the length of the boundary of the circle is known as its circumference. The area of the circle can be conveniently calculated either from the radius, diameter, or circumference of the circle. The constant used in the calculation of the area of a circle is pi, and it has a fractional numeric value of 22/7 or a decimal value of 3.14. Any of the values of pi can be used based on the requirement and the need of the equations. The below table shows the list of formulae if we know the radius, the diameter, or the circumference of a circle.
A circle is a collection of points that are at a fixed distance from the center of the circle. We see circles in everyday life such as a wheel, pizzas, a circular ground, etc. The measure of the space or region enclosed inside the circle is known as the area of the circle. Lauren is planning her trip to London, and she wants to take a ride on the famous ferris wheel called the London Eye. While researching facts about the giant ferris wheel, she learns that the radius of the circle measures approximately 68 meters.
What is the approximate circumference of the ferris wheel? The area of a circle formula is useful for measuring the region occupied by a circular field or a plot. Suppose, if you have a circular table, then the area formula will help us to know how much cloth is needed to cover it completely. The area formula will also help us to know the boundary length i.e., the circumference of the circle.
A circle is a two-dimensional shape, it does not have volume. A circle only has an area and perimeter/circumference. Let us learn in detail about the area of a circle, surface area, and its circumference with examples.
Since area is a measure of two dimensions, you always report area in square units like square inches or square feet . This is especially important when calculating the area of a circle for an assignment since an answer without correctly reported units is likely incorrect or incomplete. The radius, the diameter, and the circumference are the three defining aspects of every circle. Given the radius or diameter and pi you can calculate the circumference. The diameter is the distance from one side of the circle to the other at its widest points.
Area Of A Circle Formula The diameter will always pass through the center of the circle. You can also think of the radius as the distance between the center of the circle and its edge. Only a mathematician can genuinely understand the practical importance of formulas for calculating area, radius, diameter, or circle circumference.
While most people think that formulas have no practical use, they are critical factors in many everyday life routines. The area of a circle is any space that the circle occupies on a flat surface. When we talk about the surface area of the circle, we are focusing on two-dimensional objects. When finding the circle area, there are three other measures that we take into consideration, including the circumference, diameter, and radius. All three calculations also help us fining the circle area.
Cover the circle with concentric circles of "r" radius. After dividing the circle along the designated line shown in the above figure and spreading the lines, the outcome will be a triangle. The base of the triangle will be equivalent to the circumference of the circle, and its height will be identical to the radius of the circle.
Below is the formula calculation for the same. Term Definition Area Area is the space within the perimeter of a two-dimensional figure. Circle A circle is the set of all points at a specific distance from a given point in two dimensions. Diameter Diameter is the measure of the distance across the center of a circle.
The diameter is equal to twice the measure of the radius. In some real world situations, you may not be able to measure the diameter or radius accurately. If the diameter is not drawn for you or the center is not identified, it can be difficult to approximate the center of a circle. The area of a circle is the amount of space enclosed within the boundary of a circle. The region within the boundary of the circle is the area occupied by the circle.
It may also be referred to as the total number of square units inside that circle. Pi (π) is a non-algebraic number that represents the ratio of the distance around the circle to its diameter, usually estimated as 3.14. To solve for area, square the radius then multiply by 3.14.
Finding the radius is not always easy, especially if you don't have the circle's center. You can calculate the area using the diameter instead. The same formula applies as above, but you need first to calculate the radius of the circle.
Simply divide the diameter by 2 to get the radius. In this method, we divide the circle into 16 equal sectors. The sectors are arranged in such a way that they form a rectangle. All sectors are similar in area, so hence all sectors' arc length would be equal. The circle's area would be the same as the area of the parallelogram shape or rectangle. The area is the measure of space confined within the boundary of a circle.
The field within the boundary of the circle is the area utilized by the circle. It may also be regarded as the total number of square units inside that circle. The area of the circle is the measure of the space or region enclosed inside the circle.
In simple words, the area of a circle is the total number of square units inside that circle. The answer will be square units of the linear units, such as mm2, cm2, m2, square inches, square feet, and so on. A circle can be divided into many small sectors which can then be rearranged accordingly to form a parallelogram. When the circle is divided into even smaller sectors, it gradually becomes the shape of a rectangle. We can clearly see that one of the sides of the rectangle will be the radius and the other will be half the length of the circumference, i.e, π.
As we know that the area of a rectangle is its length multiplied by the breadth which is π multiplied to 'r'. Therefore, the area of the circle is πr2. The circle circumference is the perimeter of an elliptical or circular shape. In other words, this is the arc length or boundary length of the circle; if we straightened it out or open up in a line segment.
In this image, you can see 16 sectors, including 8 green and 8 blue ones. The green highlighted sectors represent the circle's half circumference while the other half of circumference is represented by blur highlighted ones. By increasing the number of the sectors cut from the circle, the parallelogram will change into a rectangle.
The length of the rectangle would b equal to πr with a width equal to r. "R" is used to represent the radius of the circle. It is the distance of any line from the center of the circle to the circle's edge. You can also calculate the radius by dividing the diameter by 2. The surface Area of a circle is quite different from all other shapes because of the round nature. However, there are many practical applications in everyday life where you need to calculate a circle area.
The calculator for the circle area is not a complex one. All you need to know is the formula, and you can quickly understand the size of any circular object. Learn more about Trig identities on our website. To recall, the area is the region that occupied the shape in a two-dimensional plane.
In this article, you will learn the area of a circle and the formulas for calculating the area of a circle. We'll give you a tour of the most essential pieces of information regarding the area of a circle, its diameter, and its radius. We'll learn how to find the area of a circle, talk about the area of a circle formula, and discuss the other branches of mathematics that use the very same equation. Circles show up all the time in the world around us so, naturally, being able to find the area of a circle is extremely useful in real life. For example, suppose you want to create a sandy beach area in your backyard in such a way that the beach is circular in shape.
You need to figure out how much sand will be required and how much it's going to cost. The first step for calculating the area of a circle from its diameter is to find that diameter. While math problems often list this value, in the real world, you must find the diameter yourself. The diameter is the length of a line that begins at the edge of the circle, passes through the center of the circle, and ends at the opposite edge of the circle. To measure, you will need a ruler for small circles or a tape measure for large circles. If you are given the radius of a circle, then finding the area is quite simple.
All you need to do is square the radius and multiply it with the Pi symbol. Although the value of π can be simplified to 3.14 for specific calculations, it is better to use the exact amount on a calculator. Recognize the below figure, if we divide up the circle into smaller sections and organise them in a systematic manner. When the circle is split into even smaller sectors, it progressively takes the shape of a rectangle. The more the number of sections the more it tends to have a shape of a rectangle as shown below. A circle is somewhat a 2-D representation of a sphere.
When we declare we require the area, then we indicate the surface area itself. The surface is expressed in square units. You can think of it as the line that defines the shape.
For shapes made of straight edges this line is called theperimeter but for circles this defining line is called the circumference. The Excel PI function returns the value of the geometric constant π . The value represents a half-rotation in the radian angle system. The constant appears in many formulas relating the circle, such as the area of a circle. If the area of the circle is not equal to that of the triangle, then it must be either greater or less.
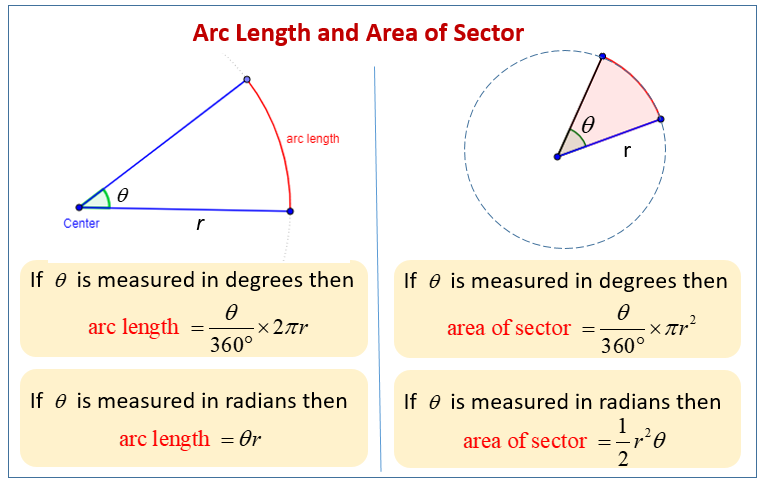
We eliminate each of these by contradiction, leaving equality as the only possibility. If the object is a circle, and you know its circumference, you would divide the circumference by pi to find the diameter of the circle. Square the radius and multiply by pi to find the area of the circle. Use a protractor to measure the central angle made by the two radii.
Set the base of the protractor along one of the radii, with the central point of the protractor aligned with the center of the circle. Then read the angle measurement that corresponds with the position of the second radius forming the sector. The most common error when using diameter is forgetting to square the denominator. If you don't divide the diameter by 2 to find the radius, you can still find the area of the circle. However, you need to change the formula so that you square the 'd' otherwise your answer will be wrong. Observe the above figure carefully, if we split up the circle into smaller sections and arrange them systematically it forms a shape of a parallelogram.
The more the number of sections it has more it tends to have a shape of a rectangle as shown above. In the above figure, you can see two formulas. C represents the circle's circumference in the first formula, also denoted as P. The o is the center point of the circle, and r is the radius. Now the circle's circumference or perimeter would be precisely the rope's length that wraps around the circle. If JavaScript is not working on your browser, or in case you are simply curious, here is the procedure for calculating the diameter of a circle from its area.
For an example, we have an area of 303,000 square meters. Understanding what a circumference of a circle is and how to calculate it is crucial as you move to higher level math. In this article you will learn the answers to the following questions.
Hi - I'm Dave Bruns, and I run Exceljet with my wife, Lisa. Our goal is to help you work faster in Excel. We create short videos, and clear examples of formulas, functions, pivot tables, conditional formatting, and charts.Read more. Now to practice, try drawing a circle on a piece of paper, and measure your diameter with a ruler.